Context Free Grammar

Context Free Grammar

Context Free grammar or CGF, G is represented by four components that is G= (V, T, P, S), where V is the set of variables, T the terminals, P the set of productions and S the start symbol.

Example: The grammar G_pal for palindromes is represented by

G_pal = ({P}, {0, 1}, A, P)

Where A represents the set of five productions

1. P→∈
2. P→0
3. P→1
4. P→0P0
5. P→1P1 

Derivation using Grammar 

Example 1: Leftmost Derivation

The inference that a * (a+b00) is in the language of variable E can be reflected in a derivation of that string, starting with the string E. Here is one such derivation:

E →E * E → I * E → a * E →a * (E) → a * (E + E) → a * (I + E) → a * (a + E) →a * (a + I) → a * (a + I0) → a * (a + I00) → a * (a + b00)

Leftmost Derivation - Tree

Example 2: Rightmost Derivations

The derivation of Example 1 was actually a leftmost derivation. Thus, we can describe the same derivation by:

E→ E * E → E *(E) → E * (E + E) →

E * (E + I) → E * (E +I0) → E * (E + I00) → E * (E + b00) →

E * (I + b00) → E * (a +b00) → I * (a + b00) → a * (a + b00)

We can also summarize the leftmost derivation by saying
E → a * (a + b00), or express several steps of the derivation by expressions such as E * E → a * (E).

Rightmost Derivation - Tree

There is a rightmost derivation that uses the same replacements for each variable, although it makes the replacements in different order. This rightmost derivation is:

E → E * E → E * (E) → E * (E + E) →

E * (E + I) → E * (E + I0) → E * (E + I00) → E * (E + b00) →

E * (I + b00) → E * (a + b00) → I * (a + b00) → a * (a + b00)

This derivation allows us to conclude E → a * (a + b00)

Consider the Grammar for string(a+b)*c

E→E + T | T

T→ T * F | F

F→ ( E ) | a | b | c

Leftmost Derivation

E→T→T*F→F*F→(E)*F→(E+T)*F→(T+T)*F→(F+T)*F →(a+T)*F →(a+F)*F →(a+b)*F→(a+b)*c

Rightmost derivation

E→T→T*F→T*c→F*c→(E)*c→(E+T)*c→(E+F)*c→(E+b)*c→(T+b)*c→(F+b)*c→(a+b)*c

Example 2:

Consider the Grammar for string (a,a)

S->(L)|a

L->L,S|S

Leftmost derivation

S→(L)→(L,S)→(S,S)→(a,S)→(a,a)

Rightmost Derivation

S→(L)→(L,S)→(L,a)→(S,a)→(a,a)

The Language of a Grammar

If G(V,T,P,S) is a CFG, the language of G, denoted by L(G), is the set of terminal strings that have derivations from the start symbol.
L(G) = {w in T | S → w}

Sentential Forms

Derivations from the start symbol produce strings that have a special role called “sentential forms”. That is if G = (V, T, P, S) is a CFG, then any string in (V → T)* such that S →a is a sentential form. If S →a, then is a left – sentential form, and if S →a , then is a right – sentential form. Note that the language L(G) is those sentential
forms that are in T*; that is they consist solely of terminals.

For example, E * (I + E) is a sentential form, since there is a derivation

E → E * E → E * (E) → E * (E + E) → E * (I + E)

However this derivation is neither leftmost nor rightmost, since at the last step, the middle E is replaced.

As an example of a left – sentential form, consider a * E, with the leftmost derivation.

E → E * E → I * E → a * E

Additionally, the derivation
E → E * E → E * (E) → E * (E + E)

Shows that
E * (E + E) is a right – sentential form.

Ambiguity

A context – free grammar G is said to be ambiguous if there exists some w ∈L(G) which has at least two distinct derivation trees. Alternatively, ambiguity implies the existence of two or more left most or rightmost derivations.

Ex:-

Consider the grammar G=(V,T,E,P) with V={E,I}, T={a,b,c,+,*,(,)}, and productions.

E→I,

E→E+E,

E→E*E,

E→(E),

I→a|b|c

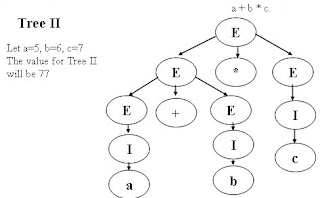
Consider two derivation trees for a + b * c.

Now unambiguous grammar for the above

Example:

E→T, T→F, F→I, E→E+T, T→T*F,

F→(E), I→a|b|c

Inherent Ambiguity
A CFL L is said to be inherently ambiguous if all its grammars are ambiguous
Example:Condider the Grammar for string aabbccdd
S→AB | C
A→ aAb | ab
B→cBd | cd
C→ aCd | aDd
D->bDc | bc

Parse tree for string aabbccdd

Applications of Context – Free Grammars

• Parsers
• The YACC Parser Generator
• Markup Languages
• XML and Document type definitions